| xi+1 = | xi  2 | + | n  2xi |
Many flash users have wanted to take advantage of the actions capabilities to do really cool things. Wouldn't it be great if you could move symbols around the screen based on geometric calculations? Well, unfortunately the only advanced mathematical functions flash 4.0 provides are Int() and Random(). Both are really useful but what we really need are Exp(), Sqrt(), Sin(), and Cos(), right? Well, you're in luck! This tutorial will show you how to do all of this stuff and more with a few simple lines of code. And don't worry, even if you don't know what a Taylor series is, you'll still be able to simply cut and paste some code right into your flash movie.
You may be asking yourself, Why would such functions be of any use to me? Well just to give you an idea of what can be done with geometry check out a flash game I made which uses all the functions described in this document.
Let's start off with an easy one. The exponent function can be accomplished via a simple loop. To calculate xn with x = 17 and n = 9 simply use the following code substituting in the correct values for x and n:
Set Variable: "x" = 17
Set Variable: "n" = 9
Set Variable: "exp" = 1
Set Variable: "count" = 0
Loop While (count < n)
Set Variable: "exp" = exp * x
Set Variable: "count" = count + 1
End Loop
After this code segment executes, the correct value of xn will be contained in the "exp" variable. Notice how if n = 0, the loop will never be executed and the value of "exp" will remain = 1. And there was only 8 lines of code!
Here's another short code segment that calculates factorials. See if you can trace through the logic for n! where n = 3.
Set Variable: "n" = 3
Set Variable: "fact" = 1
Set Variable: "count" = n
Loop While (count > 0)
Set Variable: "fact" = fact * count
Set Variable: "count" = count - 1
End Loop
Not too tough right? At the end of the execution the value of n! will be contained in the variable "fact". Again notice that if n = 0, the loop is never executed and the value of "fact" remains = 1.
All right, why don't we try something a little less obvious. The square root function can be approximated using what is known as Newton's iterative or the Babylonian method. In the following formula, n is the number whose square root must be calculated and xi+1 is the root. The accuracy depends on the number of iterations.
| xi+1 = | xi  2 | + | n  2xi |
The following code segment performs Newton's iterative. Set "square" to the number whose square root you wish to find, and "max_iteration" to whatever you want. Lower values will be less accurate but will be processed faster. Higher values will give you greater accuracy but will eat up processor time. "max_iterations" = 10 seems to give about 10 decimal places accuracy for numbers under 20,000, and is executed fast enough even on slow machines. At the end of execution, the "root" variable contains the square root of "square".
Set Variable: "square" = 11
Set Variable: "root" = 1
Set Variable: "max_iteration" = 10
Set Variable: "count" = 0
Loop While (count < max_iteration)
Set Variable: "root" = (root/2)+(square/(2*root))
Set Variable: "count" = count + 1
End Loop
There is one problem with this algorithm; it can't take the square root of zero since it would result in a division by zero. But that could be fixed with a simple if statement. See if you can work it in there. Also there are other algorithms for calculating the square root and some are more efficient than this one. But Newton's method can be coded in just 8 short lines of code which is why I chose it. No sense in cluttering up your flash movie with thousands of lines of script.
The square root is useful for calculating the distance between two points whose coordinates are (x1, y1) and (x2, y2)
distance = 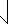 |
(x2 - x1)2 + (y2 - y1)2 |
OK, now mabye you have the confidence to tackle some real math. You can calculate the sine of any angle using the following infinite Taylor series:
| sin x = x - |
x3  3! |
+ |
x5  5! |
+ ... + (-1)n |
x2n+1     (2n+1)! |
+ ... |
If you want to know more about where this formula comes from or Taylor series' in general, go read a calculus text book. If you just want to take a sine in flash, read on.
In practice, if you just take the first several terms of this formula, you get a decent approximation of the sine function. However, x must converted from degrees to radians. No problem. The following code segment basically calculates the above formula for the sine of 30 degrees. Simply set the value of "degrees" to the angle, and the value of "max_iterations" for the desired level of accuracy. At the end of this code segment, the sine of "degrees" is contained in the "sin" variable.
Set Variable: "degrees" = 30
Set Variable: "pi" = 3.1415926535897932384626433832795
Set Variable: "radians" = pi*degrees/180
Set Variable: "max_iterations" = 10
Set Variable: "n" = 0
Set Variable: "sin" = 0
Loop While (n < max_iterations)
Set Variable: "count" = 0
Set Variable: "neg1" = 1
Loop While (count < n)
Set Variable: "neg1" = -1 * neg1
Set Variable: "count" = count + 1
End Loop
Set Variable: "count" = 0
Set Variable: "x2nplus1" = 1
Loop While (count < 2*n + 1)
Set Variable: "x2nplus1" = x2nplus1 * radians
Set Variable: "count" = count + 1
End Loop
Set Variable: "count" = 2*n + 1
Set Variable: "factorial" = 1
Loop While (count > 0)
Set Variable: "factorial" = factorial * count
Set Variable: "count" = count - 1
End Loop
Set Variable: "sin" = sin + neg1 * (x2nplus1/factorial)
Set Variable: "n" = n+1
End Loop
The cosine has a similar Taylor series which looks like this:
| cos x = 1 - |
x2  2! |
+ |
x4  4! |
+ ... + (-1)n |
x2n   (2n)! |
+ ... |
...And can be calculated using the following lines of code:
Set Variable: "degrees" = 30
Set Variable: "pi" = 3.1415926535897932384626433832795
Set Variable: "radians" = pi*degrees/180
Set Variable: "max_iterations" = 10
Set Variable: "n" = 0
Set Variable: "cos" = 0
Loop While (n < max_iterations)
Set Variable: "count" = 0
Set Variable: "neg1" = 1
Loop While (count < n)
Set Variable: "neg1" = -1 * neg1
Set Variable: "count" = count + 1
End Loop
Set Variable: "count" = 0
Set Variable: "x2n" = 1
Loop While (count < 2*n)
Set Variable: "x2n" = x2n * radians
Set Variable: "count" = count + 1
End Loop
Set Variable: "count" = 2*n
Set Variable: "factorial" = 1
Loop While (count > 0)
Set Variable: "factorial" = factorial * count
Set Variable: "count" = count - 1
End Loop
Set Variable: "cos" = cos + neg1 * (x2n/factorial)
Set Variable: "n" = n+1
End Loop
At the end of execution, the cosine of "degrees" will be contained in "cos". Notice the similarities between the sin and cos algorithm. And notice how they both use the exp and fact functions in their calculations. Or, if you could care less, simply cut and paste the code into your flash movie.
Once the sine and cosine are calculated, you can easily calculate all the other trigenometric functions from them with the following formulas:
| Function | Formula | Action Script | ||||
| tangent |
|
Set Variable: "tan" = sin/cos | ||||
| secant |
| Set Variable: "sec" = 1/sin | ||||
| cosecant |
| Set Variable: "csc" = 1/cos | ||||
| cotangent |
| Set Variable: "cot" = cos/sin |
Be careful about dividing by zero when calculating these. You should definately do a check first to see if the denominator in any of the above equations is equal or close to zero. Here is a sample open source flash movie that calculates all the trig functions. Download it and adjust it to suit your needs.
Note: you may be puzzled by results if you use Flash's GetProperty("target", _rotation) to define the degrees variable. For some odd reason, I have noticed that even if you set the angle using SetProperty("target", _rotation) to a round number such as 45 degrees, flash has the tendency to report back the _rotation property as 44.565633 or something close to, but not quite dead on. In most applications, the difference is negligable though.
I hope you found this tutorial useful in your flashing! I imagine version 5.0 of Flash will contain all the functions described in this tutorial and this entire document will be rendered obsolete. But until then, everything you need to know is here! Flash on...